 login/create account
login/create account
Magic square of squares ★★
Author(s): LaBar
Question Does there exist a 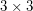 magic square composed of distinct perfect squares?
magic square composed of distinct perfect squares?
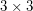 magic square composed of distinct perfect squares?
magic square composed of distinct perfect squares? Keywords:
Diophantine quintuple conjecture ★★
Author(s):
Definition A set of m positive integers 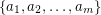 is called a Diophantine
is called a Diophantine  -tuple if
-tuple if 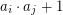 is a perfect square for all
is a perfect square for all 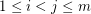 .
.
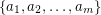 is called a Diophantine
is called a Diophantine  -tuple if
-tuple if 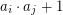 is a perfect square for all
is a perfect square for all 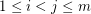 .
. Conjecture (1) Diophantine quintuple does not exist.
It would follow from the following stronger conjecture [Da]:
Conjecture (2) If 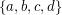 is a Diophantine quadruple and
is a Diophantine quadruple and 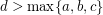 , then
, then 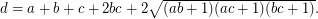
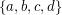 is a Diophantine quadruple and
is a Diophantine quadruple and 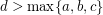 , then
, then 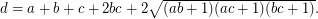
Keywords:
Inverse Galois Problem ★★★★
Author(s): Hilbert
Conjecture Every finite group is the Galois group of some finite algebraic extension of 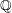 .
.
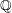 .
. Keywords:
On Gersgorin Theorem ★★
Author(s):
Gersgorin theorem states that: all the eigenvalues of ![$ A=[a_{ij}]\in M_n $](/files/tex/f871e0e7c9a9a6ce437fbea5a847f5b304447990.png) are located in the union of
are located in the union of  discs
discs 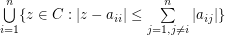 . For some special matrices, the region can be confined to
. For some special matrices, the region can be confined to 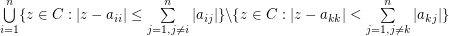 for some
for some 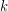 . I wonder if the new region above is valid in general?
. I wonder if the new region above is valid in general?
Keywords:
trace inequality ★★
Author(s):
Let 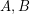 be positive semidefinite, by Jensen's inequality, it is easy to see
be positive semidefinite, by Jensen's inequality, it is easy to see ![$ [tr(A^s+B^s)]^{\frac{1}{s}}\leq [tr(A^r+B^r)]^{\frac{1}{r}} $](/files/tex/f5fa90ccf8c1dde9b9bf1f21399b3b5428dab81d.png) , whenever
, whenever 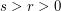 .
.
What about the 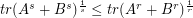 , is it still valid?
, is it still valid?
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University