 login/create account
login/create account
Diophantine quintuple conjecture
Definition A set of m positive integers 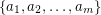 is called a Diophantine
is called a Diophantine  -tuple if
-tuple if 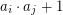 is a perfect square for all
is a perfect square for all 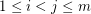 .
.
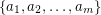 is called a Diophantine
is called a Diophantine  -tuple if
-tuple if 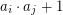 is a perfect square for all
is a perfect square for all 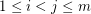 .
. Conjecture (1) Diophantine quintuple does not exist.
It would follow from the following stronger conjecture [Da]:
Conjecture (2) If 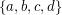 is a Diophantine quadruple and
is a Diophantine quadruple and 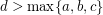 , then
, then 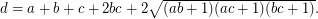
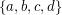 is a Diophantine quadruple and
is a Diophantine quadruple and 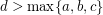 , then
, then 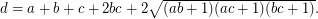
It was proved in [Db] that there are only finitely many Diophantine quintuples and no Diophantine sextuples.
Conjecture (2) is motivated by an observation of [AHS] that every Diophantine triple 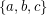 can be extended to a Diophantine quadruple
can be extended to a Diophantine quadruple 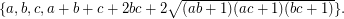
Bibliography
[Da] A. Dujella Diophantine  -tuples, a survey of the main problems and results concerning Diophantine m-tuples.
-tuples, a survey of the main problems and results concerning Diophantine m-tuples.
[Db] A. Dujella, There are only finitely many Diophantine quintuples, J. Reine Angew. Math. 566 (2004), 183-214.
[AHS] J. Arkin, V. E. Hoggatt and E. G. Strauss, On Euler's solution of a problem of Diophantus, Fibonacci Quart. 17 (1979), 333-339.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
This result has been proven
in a paper announced in 2016 and published in 2019, He, Togbé and Ziegler [350] gave the proof of the Diophantine quintuple conjecture