 login/create account
login/create account
 .
.
This problem is one of the greatest open problems in group theory. Hilbert was the first to study it in earnest. His irreducibility theorem established a connection between Galois groups over 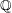 and Galois groups over
and Galois groups over 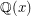 ; the latter could be attacked by geometric methods, and in this way, Hilbert showed that the symmetric and alternating groups are Galois realizable over
; the latter could be attacked by geometric methods, and in this way, Hilbert showed that the symmetric and alternating groups are Galois realizable over 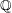 . In the 1950's, Shafarevich showed using number-theoretic methods that all finite solvable groups are Galois realizable over
. In the 1950's, Shafarevich showed using number-theoretic methods that all finite solvable groups are Galois realizable over 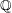 . Another spectacular result was John Thompson's realization of the Monster group as a Galois group over
. Another spectacular result was John Thompson's realization of the Monster group as a Galois group over 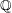 . One of Thompson's main tools was a concept he called "rigidity", a concept discovered independently by several people that continues to be important to this day. It is now known that 25 of the 26 sporadic simple groups are Galois realizable over
. One of Thompson's main tools was a concept he called "rigidity", a concept discovered independently by several people that continues to be important to this day. It is now known that 25 of the 26 sporadic simple groups are Galois realizable over 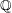 (the sole exception being the Mathieu group
(the sole exception being the Mathieu group 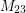 ).
).
Bibliography
[MM] Gunter Malle and B. Heinrich Matzat, Inverse Galois Theory, Springer, 1999.
[V] Helmut Völklein, Groups as Galois Groups: An introduction, Cambridge University Press, 1996.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University