 login/create account
login/create account
Convex Polygons
Erdös-Szekeres conjecture ★★★
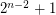 points in the plane in general position contains a subset of
points in the plane in general position contains a subset of  points which form a convex
points which form a convex  -gon.
-gon. Keywords: combinatorial geometry; Convex Polygons; ramsey theory
Convex 'Fair' Partitions Of Convex Polygons ★★
Author(s): Nandakumar; Ramana
Basic Question: Given any positive integer n, can any convex polygon be partitioned into n convex pieces so that all pieces have the same area and same perimeter?
Definitions: Define a Fair Partition of a polygon as a partition of it into a finite number of pieces so that every piece has both the same area and the same perimeter. Further, if all the resulting pieces are convex, call it a Convex Fair Partition.
Questions: 1. (Rephrasing the above 'basic' question) Given any positive integer n, can any convex polygon be convex fair partitioned into n pieces?
2. If the answer to the above is "Not always'', how does one decide the possibility of such a partition for a given convex polygon and a given n? And if fair convex partition is allowed by a specific convex polygon for a give n, how does one find the optimal convex fair partition that minimizes the total length of the cut segments?
3. Finally, what could one say about higher dimensional analogs of this question?
Conjecture: The authors tend to believe that the answer to the above 'basic' question is "yes". In other words they guess: Every convex polygon allows a convex fair partition into n pieces for any n
Keywords: Convex Polygons; Partitioning

 Drupal
Drupal CSI of Charles University
CSI of Charles University