Home » Subject » Number Theory

Odd perfect numbers

Importance: High ✭✭✭
Author(s): Ancient/folklore
Subject: Number Theory
Keywords: perfect number
Recomm. for undergrads: yes
Posted by: azi
on: September 27th, 2008
Conjecture   There is no odd perfect number.

There is substantial literature on the problem. Most proceeds from a study of the multiplicative function 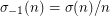$ \sigma_{-1}(n)=\sigma(n)/n $ where the conjecture can be stated: 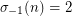$ \sigma_{-1}(n)=2 $ implies that $ n $ is even.

Bibliography



* indicates original appearance(s) of problem.
add new comment

limiting divisors

On December 7th, 2011 Anonymous says:

My idea is to assume that the OPN is divisible by a prime number (e.x. 3) then use the properties of perfect numbers to figure out other numbers the OPN is divisible by.

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.