 login/create account
login/create account
¿Are critical k-forests tight? ★★
Author(s): Strausz
Conjecture
Let 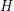 be a
be a 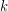 -uniform hypergraph. If
-uniform hypergraph. If 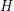 is a critical
is a critical 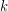 -forest, then it is a
-forest, then it is a 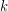 -tree.
-tree.
Keywords: heterochromatic number
Bigger cycles in cubic graphs ★★
Author(s):
Problem Let  be a cyclically 4-edge-connected cubic graph and let
be a cyclically 4-edge-connected cubic graph and let 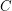 be a cycle of
be a cycle of  . Must there exist a cycle
. Must there exist a cycle 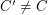 so that
so that 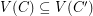 ?
?
 be a cyclically 4-edge-connected cubic graph and let
be a cyclically 4-edge-connected cubic graph and let 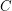 be a cycle of
be a cycle of  . Must there exist a cycle
. Must there exist a cycle 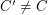 so that
so that 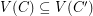 ?
? The intersection of two perfect matchings ★★
Conjecture Every bridgeless cubic graph has two perfect matchings 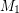 ,
, 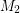 so that
so that 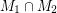 does not contain an odd edge-cut.
does not contain an odd edge-cut.
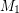 ,
, 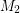 so that
so that 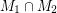 does not contain an odd edge-cut.
does not contain an odd edge-cut. Keywords: cubic; nowhere-zero flow; perfect matching
Reloid corresponding to funcoid is between outward and inward reloid ★★
Author(s): Porton
Keywords: funcoid; inward reloid; outward reloid; reloid
Distributivity of union of funcoids corresponding to reloids ★★
Author(s): Porton
Keywords: funcoid; infinite distributivity; reloid

 and
and 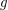 having the same source and destination
having the same source and destination ![\[ ( \mathsf{\tmop{RLD}})_{\tmop{out}} f \subseteq g \subseteq ( \mathsf{\tmop{RLD}})_{\tmop{in}} f \Leftrightarrow ( \mathsf{\tmop{FCD}}) g = f. \]](/files/tex/def032a20d7d57db67d77c0f002f1c9f2909fe98.png)
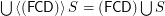 if
if 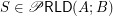 is a set of
is a set of 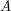 to a set
to a set 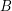 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University