 login/create account
login/create account
Linear Hypergraphs with Dimension 3 ★★
Author(s): de Fraysseix; Ossona de Mendez; Rosenstiehl
Keywords: Hypergraphs
Editorial policy
To ensure that the Garden is a high quality resource, we reserve the right to move submitted open problems to an alternate location on our site. These Second tier problems can be found by clicking the More link in the Navigate menu. When considering submissions, we take into account the value of the question, its relevance, and clarity of the exposition. Still, some of these Second tier problems can be an interesting exercise, or a worthy (but inadequately presented) question. Our editors (called greenthumbs) are listed below.
- Greenthumbs
- Matt DeVos
- Robert Samal
Big Line or Big Clique in Planar Point Sets ★★
Let  be a set of points in the plane. Two points
be a set of points in the plane. Two points  and
and  in
in  are visible with respect to
are visible with respect to  if the line segment between
if the line segment between  and
and  contains no other point in
contains no other point in  .
.
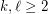 there is an integer
there is an integer  such that every set of at least
such that every set of at least  points in the plane contains at least
points in the plane contains at least 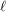 collinear points or
collinear points or  pairwise visible points.
pairwise visible points. Keywords: Discrete Geometry; Geometric Ramsey Theory

 Drupal
Drupal CSI of Charles University
CSI of Charles University