login/create account
Conjecture Any linear hypergraph with incidence poset of dimension at most 3 is the intersection hypergraph of a family of triangles and segments in the plane.
A hypergraph is linear if any two edges may share at most one vertex. The incidence poset of a hypergraph is the vertex-edge inclusion poset. The dimension of a poset 
is the minimum number of linear extentions of , whose intersection is [DM].
Schnyder proved that the incidence poset of a graph 
has dimension at most 
if and only if is planar [S89]. Fraysseix, Rosenstiehl and Ossona de Mendez proved that every planar graph has a representation by contacts of triangles [FOR94] and Scheinerman conjectured that every planar graph has a representation by intersection of segments [S84] (claimed to be proved by Gonçalves et al.).
A hypergraph is planar if its vertex-edge incidence graph is planar [W]. Fraysseix, Rosenstiehl and Ossona de Mendez proved that every planar linear hypergraph has a representation by contacts of triangles [FOR07] and it has been conjectured that they have a representation by intersection of straight line segments [FO07] (cf Straight line representation of planar linear hypergraphs).
Although the incidence poset of a simple planar hypergraph has dimension at most (what follows from [BT]), the converse is false: The linear hypergraph with vertices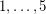 
and edge set 
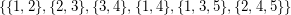has incidence dimension but is not planar (its vertex-edge incidence graph is a subdivision of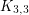 
). It follows from [O] that the vertices of simple hypergraphs with incidence posets of dimensions 
can be represented by convex sets of the Euclidean space of dimension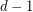 
, in such a way that the edges of the hypergraph are exactly the maximal subsets of vertices, such that the corresponding subset of convexes has a non-empty intersection.
Bibliography
[BT] G.~Brightwell and W.T. Trotter, The order dimension of planar maps, SIAM journal on Discrete Mathematics 10 (1997), no.~4, 515--528.
[DM] B.~Dushnik and E.W. Miller, Partially ordered sets, Amer. J. Math. 63 (1941), 600--610.
[FO07] Hubert de Fraysseix, Patrice Ossona de Mendez: Stretching of Jordan arc contact systems, Discrete Applied Mathematics 155 (2007), no. 9, 1079--1095.
[FOR94] H.~de Fraysseix, P.~Ossona~de Mendez, and P.~Rosenstiehl, On triangle contact graphs, Combinatorics, Probability and Computing 3 (1994), 233--246.
*[FOR07] H.~de Fraysseix, P.~Ossona~de Mendez, and P.~Rosenstiehl, Representation of Planar Hypergraphs by Contacts of Triangles, Proc. of Graph Drawing '07, to appear.
[O] P.~Ossona~de Mendez, Realization of posets, Journal of Graph Algorithms and Applications 6 (2002), no.~1, 149--153.
[S84] E.R. Scheinerman, Intersection classes and multiple intersection parameters of graphs, Ph.D. thesis, Princeton University, 1984.
[S89] W.~Schnyder, Planar graphs and poset dimension, Order 5 (1989), 323--343.
[W] T.R.S. Walsh, Hypermaps versus bipartite maps, J. Combinatorial Theory 18(B) (1975), 155--163.
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University