 login/create account
login/create account
Bigger cycles in cubic graphs (Solved)
 be a cyclically 4-edge-connected cubic graph and let
be a cyclically 4-edge-connected cubic graph and let  be a cycle of
be a cycle of  . Must there exist a cycle
. Must there exist a cycle 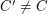 so that
so that 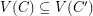 ?
? The main interest in this problem is that an affirmative solution would imply the Cycle double cover conjecture. The idea behind this is an old one - probably due to Seymour - which shall be described below. I (M. DeVos) regard this problem as folklore, which is why I haven't listed an author.
One sensible approach to the cycle double cover conjecture is that described in Faithful cycle covers. Quickly, the idea here is to consider a more general problem.. given a graph  and a map
and a map 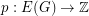 , say that a list of cycles of
, say that a list of cycles of  is a
is a  -cover if every edge
-cover if every edge  appears in exactly
appears in exactly 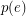 cycles from the list. Now, we are interested in what properties guarantee the existence of a
cycles from the list. Now, we are interested in what properties guarantee the existence of a  -cover. The Cycle double cover conjecture asserts that a
-cover. The Cycle double cover conjecture asserts that a  -cover exists whenever
-cover exists whenever  is bridgeless and
is bridgeless and  is constantly 2. Another interesting special case is when
is constantly 2. Another interesting special case is when  is a bridgeless cubic graph, the range of
is a bridgeless cubic graph, the range of  is a subset of
is a subset of 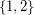 , and
, and 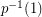 is a union of (edge sets of) cycles. It might be tempting to hope that under these assumptions a
is a union of (edge sets of) cycles. It might be tempting to hope that under these assumptions a  -cover would always exist, but this is false.. if
-cover would always exist, but this is false.. if  is the Petersen graph and
is the Petersen graph and  has weight 2 on a perfect matching and 1 elsewhere, then there is no
has weight 2 on a perfect matching and 1 elsewhere, then there is no  -cover. In this weighting, the edges of weight 1 form two cycles. The following conjecture asserts that no such example exists if the edges of weight 1 form a single cycle.
-cover. In this weighting, the edges of weight 1 form two cycles. The following conjecture asserts that no such example exists if the edges of weight 1 form a single cycle.
 be a bridgeless cubic graph, let
be a bridgeless cubic graph, let 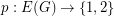 and assume that
and assume that 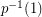 is a cycle
is a cycle  . Then there exists a
. Then there exists a  -cover of
-cover of  .
. This conjecture is equivalent to the assertion that for every bridgeless cubic graph  and every cycle
and every cycle  of
of  , there exists a cycle double cover of
, there exists a cycle double cover of  using
using  . So, in particular, it implies the cycle double cover conjecture. An affirmative solution to the main problem on this page would imply this conjecture (and thus cycle double cover). Let us ignore the details about edge connectivity (the ideas here are standard - and easy to find) and state the main idea behind this implication. The trick is to proceed by induction (say on
. So, in particular, it implies the cycle double cover conjecture. An affirmative solution to the main problem on this page would imply this conjecture (and thus cycle double cover). Let us ignore the details about edge connectivity (the ideas here are standard - and easy to find) and state the main idea behind this implication. The trick is to proceed by induction (say on 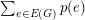 ), then choose a cycle
), then choose a cycle 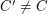 so that
so that 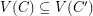 , and consider
, and consider 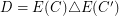 (symmetric difference). Note that
(symmetric difference). Note that  is a union of cycles (which we will eventually use in our cover). Next, modify
is a union of cycles (which we will eventually use in our cover). Next, modify  and
and  to form
to form 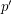 and
and 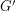 by decreasing the weight of every edge in
by decreasing the weight of every edge in  and then deleting edges of weight 0. An easy check shows that
and then deleting edges of weight 0. An easy check shows that 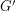 is a subdivision of a bridgeless cubic graph, and
is a subdivision of a bridgeless cubic graph, and 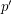 is a weight function on
is a weight function on 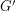 which has weight 1 on
which has weight 1 on 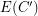 . So, by induction, we find a
. So, by induction, we find a 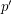 -cover of
-cover of 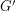 . Now adding back the cycles formed by
. Now adding back the cycles formed by  gives us a
gives us a  -cover of
-cover of  .
.
Although the problem looks a bit greedy, it is true in a number of special cases. First off, if  is a Hamiltonian cycle of
is a Hamiltonian cycle of  , then Smith's theorem shows that
, then Smith's theorem shows that  has another Hamiltonian cycle
has another Hamiltonian cycle 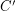 (which obviously satisfies the condition
(which obviously satisfies the condition 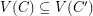 ). A somewhat more subtle application of the same theorem shows that the problem also has an affirmative answer when
). A somewhat more subtle application of the same theorem shows that the problem also has an affirmative answer when 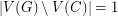 . If we drop the assumption of cyclic 4-edge-connectivity, there is a counterexample
. If we drop the assumption of cyclic 4-edge-connectivity, there is a counterexample 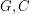 where
where 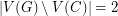 which is based on gluing two Petersen graphs together at a vertex. However, as far as we know, the only such examples have nontrivial 3-edge-cuts.
which is based on gluing two Petersen graphs together at a vertex. However, as far as we know, the only such examples have nontrivial 3-edge-cuts.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
This conjecture is false
In the paper "Stable dominating circuits in snarks" (Discrete Math 233 (247-256) 2001) Martin Kochhol gives a counter example to this conjecture (in fact he gives an infinite family of them).
Using computer search I have found even smaller counter examples (the smallest has just 20 vertices).
Best regards,
Jonas Hägglund