 login/create account
login/create account
Partial List Coloring ★★★
Author(s): Albertson; Grossman; Haas
Conjecture Let  be a simple graph with
be a simple graph with  vertices and list chromatic number
vertices and list chromatic number 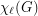 . Suppose that
. Suppose that 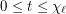 and each vertex of
and each vertex of  is assigned a list of
is assigned a list of  colors. Then at least
colors. Then at least 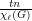 vertices of
vertices of  can be colored from these lists.
can be colored from these lists.
 be a simple graph with
be a simple graph with  vertices and list chromatic number
vertices and list chromatic number 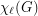 . Suppose that
. Suppose that 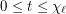 and each vertex of
and each vertex of  is assigned a list of
is assigned a list of  colors. Then at least
colors. Then at least 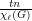 vertices of
vertices of  can be colored from these lists.
can be colored from these lists. Keywords: list assignment; list coloring
Combinatorial covering designs ★
Author(s): Gordon; Mills; Rödl; Schönheim
A 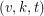 covering design, or covering, is a family of
covering design, or covering, is a family of  -subsets, called blocks, chosen from a
-subsets, called blocks, chosen from a  -set, such that each
-set, such that each  -subset is contained in at least one of the blocks. The number of blocks is the covering’s size, and the minimum size of such a covering is denoted by
-subset is contained in at least one of the blocks. The number of blocks is the covering’s size, and the minimum size of such a covering is denoted by 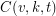 .
.
Problem Find a closed form, recurrence, or better bounds for 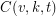 . Find a procedure for constructing minimal coverings.
. Find a procedure for constructing minimal coverings.
 . Find a procedure for constructing minimal coverings.
. Find a procedure for constructing minimal coverings. Keywords: recreational mathematics
Burnside problem ★★★★
Author(s): Burnside
Conjecture If a group has  generators and exponent
generators and exponent  , is it necessarily finite?
, is it necessarily finite?
 generators and exponent
generators and exponent  , is it necessarily finite?
, is it necessarily finite? Keywords:
Inscribed Square Problem ★★
Author(s): Toeplitz
Conjecture Does every Jordan curve have 4 points on it which form the vertices of a square?
Keywords: simple closed curve; square

 Drupal
Drupal CSI of Charles University
CSI of Charles University