 login/create account
login/create account
Total Colouring Conjecture ★★★
Author(s): Behzad
Conjecture A total coloring of a graph 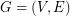 is an assignment of colors to the vertices and the edges of
is an assignment of colors to the vertices and the edges of  such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph
such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph  ,
, 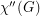 , equals the minimum number of colors needed in a total coloring of
, equals the minimum number of colors needed in a total coloring of  . It is an old conjecture of Behzad that for every graph
. It is an old conjecture of Behzad that for every graph  , the total chromatic number equals the maximum degree of a vertex in
, the total chromatic number equals the maximum degree of a vertex in  ,
, 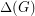 plus one or two. In other words,
plus one or two. In other words, ![\[\chi''(G)=\Delta(G)+1\ \ or \ \ \Delta(G)+2.\]](/files/tex/d4ea30e930ec20e02c5a03c6322e6d99a6bdb63a.png)
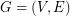 is an assignment of colors to the vertices and the edges of
is an assignment of colors to the vertices and the edges of  such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph
such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph  ,
, 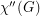 , equals the minimum number of colors needed in a total coloring of
, equals the minimum number of colors needed in a total coloring of  . It is an old conjecture of Behzad that for every graph
. It is an old conjecture of Behzad that for every graph  , the total chromatic number equals the maximum degree of a vertex in
, the total chromatic number equals the maximum degree of a vertex in  ,
, 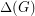 plus one or two. In other words,
plus one or two. In other words, ![\[\chi''(G)=\Delta(G)+1\ \ or \ \ \Delta(G)+2.\]](/files/tex/d4ea30e930ec20e02c5a03c6322e6d99a6bdb63a.png)
Keywords: Total coloring
Hedetniemi's Conjecture ★★★
Author(s): Hedetniemi
Conjecture If 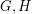 are simple finite graphs, then
are simple finite graphs, then  .
.
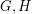 are simple finite graphs, then
are simple finite graphs, then  .
. Here 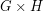 is the tensor product (also called the direct or categorical product) of
is the tensor product (also called the direct or categorical product) of  and
and  .
.
Keywords: categorical product; coloring; homomorphism; tensor product
Edge Reconstruction Conjecture ★★★
Author(s): Harary
Conjecture
Every simple graph with at least 4 edges is reconstructible from it's edge deleted subgraphs
Keywords: reconstruction

 Drupal
Drupal CSI of Charles University
CSI of Charles University