 login/create account
login/create account
Conjecture Let  be a simple graph with
be a simple graph with  vertices and list chromatic number
vertices and list chromatic number 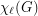 . Suppose that
. Suppose that 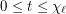 and each vertex of
and each vertex of  is assigned a list of
is assigned a list of  colors. Then at least
colors. Then at least 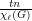 vertices of
vertices of  can be colored from these lists.
can be colored from these lists.
 be a simple graph with
be a simple graph with  vertices and list chromatic number
vertices and list chromatic number 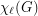 . Suppose that
. Suppose that 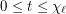 and each vertex of
and each vertex of  is assigned a list of
is assigned a list of  colors. Then at least
colors. Then at least 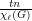 vertices of
vertices of  can be colored from these lists.
can be colored from these lists. Albertson, Grossman, and Haas introduce this interesting question in [AGH], and prove some partial results. For instance, they show that under the above assumptions, at least 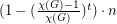 vertices of
vertices of  can be colored from the lists.
can be colored from the lists.
Bibliography
*[AGH] M. Albertson, S. Grossman and R. Haas, Partial list colouring, Discrete Math., 214(2000), pp. 235-240.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University