login/create account
Inscribed Square Problem
Conjecture Does every Jordan curve have 4 points on it which form the vertices of a square?
A Jordan curve is a continuous function 
from the closed interval ![$ [0,1] $](/files/tex/f65c588a56e7eca31976481db4eeeae4e72a4d3a.png)
to the plane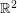 
with the properties that is injective on the half-open interval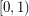 
(i.e., is simple) and 
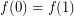(i.e., is closed).
Bibliography
[M] Meyerson, M.D., Equilateral triangles and continuous curves, Fund. Math. 110, (1980), 1--9.
* indicates original appearance(s) of problem.
inscription of squares in simple closed curves
On March 3rd, 2010 Anonymous says:
There is a theorem that says:
in all simple closed curves there are 4n points that are vertex of n squares (inf = > n > =1)
Jorge Pasin.
in all simple closed curves there are 4n points
On November 8th, 2010 Anonymous says:
Would you clarify? An obtuse triangle has only one inscribed square, so this theorem is not true for n>=2. Do you have a reference to this theorem? Strashimir Popvassilev
Is the conjecture known to
On November 25th, 2009 Anonymous says:
Is the conjecture known to be true for C^1-smooth curves?
no.
On June 2nd, 2010 Anonymous says:
If it were true for C^1 curves, then since a Jordan curve is compact, it may be weierstrass approximated by a series of C^1 curves (indeed by curves whose component functions are polynomials) such that the series converges uniformly to the given jordan curve. Then by assumption, each curve in the sequence contains 4 points forming a square, and the sequence of squares can be regarded as (eventually) a sequence in the (sequentially) compact space of the 4-fold product of any closed epsilon enlargement of the area bounded by the original jordan curve. It follows that the sequence of squares contains a convergent subsequence, which can be shown to be a square lying on the original jordan curve.
Thus, proving the C^1 case proves the general case.
This is flawed
On June 7th, 2010 Anonymous says:
The approximation argument is flawed: the squares on approximating curves may have sides decreasing to 0, in which case the limiting "square" degenerates to a point. In fact, Stromquist's theorem covers a much wider class of curves than C^1, but not all continuous curves.
Quantifier
On April 28th, 2008 Anonymous says:
Phrasing should be changed from "Does any..." to "Does every..."
Drupal
CSI of Charles University
Already solved
This was proven in https://arxiv.org/pdf/2005.09193.pdf