login/create account
Schanuel's Conjecture
Conjecture Given any 
complex numbers 
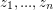which are linearly independent over the rational numbers 
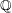, then the extension field 
has transcendence degree of at least over .
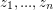complex numbers which are linearly independent over the rational numbers 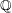, then the extension field has transcendence degree of at least over .
Schanuel's Conjecture implies the algebraic independence of 
and 
, as well as a positive solution to Tarski's exponential function problem.
Bibliography
* indicates original appearance(s) of problem.
Re: I must agree with the
On January 19th, 2010 Robert Samal says:
Encouraged by the previous comments, I changed the rating of this problem and the "mimic" one. Thanks for the feedback.
from Gasses
On December 27th, 2009 Anonymous says:
I am just curious why 'importance' is given as 2 stars when (according to wikipedia) "The conjecture, if proven, would subsume most known results in transcendental number theory." Some of these results include results on this page that have greater importance than 2 stars.
Drupal
CSI of Charles University
I must agree with the
I must agree with the previous comment. Schanuel's conjecture is likely the most important open problem in Transcendental Number Theory. I realize that this might not be as major a field as the study of "mimic" numbers, but.....