 login/create account
login/create account
Conjecture Given any  complex numbers
complex numbers 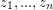 which are linearly independent over the rational numbers
which are linearly independent over the rational numbers 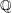 , then the extension field
, then the extension field 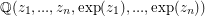 has transcendence degree of at least
has transcendence degree of at least  over
over 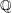 .
.
 complex numbers
complex numbers 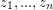 which are linearly independent over the rational numbers
which are linearly independent over the rational numbers 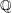 , then the extension field
, then the extension field 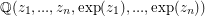 has transcendence degree of at least
has transcendence degree of at least  over
over 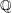 .
.
Schanuel's Conjecture implies the algebraic independence of  and
and  , as well as a positive solution to Tarski's exponential function problem.
, as well as a positive solution to Tarski's exponential function problem.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University