 login/create account
login/create account
Hamiltonian cycles in line graphs of infinite graphs
- \item If
 is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph
is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph 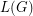 of a locally finite graph
of a locally finite graph  is 4-connected, then
is 4-connected, then 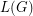 is hamiltonian.
is hamiltonian. (Reproduced from [M].)
A locally finite graph is hamiltonian, if its Freudenthal compactification (also called the end compactification, see [D]) contains a hamilton circle, i.e. a homeomorphic copy of 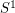 containing all vertices.
containing all vertices.
The first part is known for finite graphs. The proof uses the existence of two edge-disjoint spanning trees in 4-edge-connected graphs. In the infinite case, it would be enough to prove that a 4-edge-connected locally finite graph  has two edge-disjoint topological spanning trees (see [D]), one of which is connected as a subgraph of
has two edge-disjoint topological spanning trees (see [D]), one of which is connected as a subgraph of  . The problem is open even for the 1-ended case (where hamilton circles correspond to 2-way-infinite paths).
. The problem is open even for the 1-ended case (where hamilton circles correspond to 2-way-infinite paths).
The second part is widely open even in the finite case, where it was proposed by Thomassen [T].
Bibliography
[D] Reinhard Diestel, Graph Theory, Third Edition, Springer, 2005.
*[G] A. Georgakopoulos, Oberwolfach reports, 2007.
[M] Bojan Mohar, Problem of the Month
[T] Carsten Thomassen, Reflections on graph theory, J. Graph Theory 10 (1986) 309-324, MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University