 login/create account
login/create account
Friendly partitions
A friendly partition of a graph is a partition of the vertices into two sets so that every vertex has at least as many neighbours in its own class as in the other.
 , all but finitely many
, all but finitely many  -regular graphs have friendly partitions?
-regular graphs have friendly partitions? Let me say at the start, that I (M. DeVos) suspect this problem has been considered previously, so I await a more correct attribution.
An unfriendly partition of a graph is a partition of the vertices into two sets so that every vertex has at least as many neighbours in the opposite class as its own. It is an easy fact that every (finite) graph has an unfriendly partition; for instance, any maximum size edge-cut gives a partition with this property.
Finding friendly partitions appears to be considerably more difficult. Perhaps one reason why is that there exist graphs without unfriendly partitions. For instance, 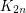 and
and 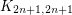 have no unfriendly partitions. However, it appears possible that the only graphs which fail to have friendly partitions are fairly dense.
have no unfriendly partitions. However, it appears possible that the only graphs which fail to have friendly partitions are fairly dense.
When 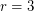 , the above problem is fairly easy to solve, as it reduces to the problem of finding two vertex disjoint cycles. Every cubic graph other than
, the above problem is fairly easy to solve, as it reduces to the problem of finding two vertex disjoint cycles. Every cubic graph other than 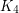 or
or 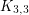 has two disjoint cycles, and thus has a friendly partition. The case when
has two disjoint cycles, and thus has a friendly partition. The case when 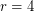 is also not terribly complicated. However, the next step up,
is also not terribly complicated. However, the next step up, 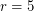 looks like a tricky problem which requires something new.
looks like a tricky problem which requires something new.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Name of the problem
In the bibliography, this is known as Satisfactory graph partition or Internal graph partition.