 login/create account
login/create account
3-Edge-Coloring Conjecture
Conjecture Suppose  with
with 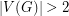 is a connected cubic graph admitting a
is a connected cubic graph admitting a  -edge coloring. Then there is an edge
-edge coloring. Then there is an edge 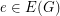 such that the cubic graph homeomorphic to
such that the cubic graph homeomorphic to 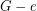 has a
has a  -edge coloring.
-edge coloring.
 with
with 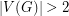 is a connected cubic graph admitting a
is a connected cubic graph admitting a  -edge coloring. Then there is an edge
-edge coloring. Then there is an edge 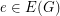 such that the cubic graph homeomorphic to
such that the cubic graph homeomorphic to 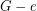 has a
has a  -edge coloring.
-edge coloring. Reformulation via 4-flows:
Conjecture Suppose  is a cubic graph with a nowhere-zero
is a cubic graph with a nowhere-zero 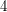 -flow, then there is an edge
-flow, then there is an edge 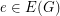 such that
such that 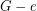 has a nowhere-zero
has a nowhere-zero 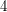 -flow.
-flow.
 is a cubic graph with a nowhere-zero
is a cubic graph with a nowhere-zero 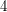 -flow, then there is an edge
-flow, then there is an edge 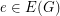 such that
such that 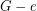 has a nowhere-zero
has a nowhere-zero 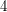 -flow.
-flow. Bibliography
* indicates original appearance(s) of problem.
question
On June 22nd, 2022 Anonymous says:
wouldn't removing any edge from a cubic graph make the graph not cubic?
A counterexample?
On August 3rd, 2021 Anonymous says:
What would be the cubic graph homeomorphic to K4-e? I think I can show there does not exist a cubic graph homeomorphic to K4-e. If so, this would seem to contradict the conjecture's claim.
Is there yet any progress on this problem?
On November 13th, 2020 Anonymous says:
Hello, I would like to know whether anybody made any progress on this. I tried to google and found nothing. Also, why is there nothing in Bibliography of this problem? Is there any paper involving or proposing it? Thanks in advance

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Context
Is this conjecture missing some greater context? It seems obviously false on its own