 login/create account
login/create account
Hoffmann-Ostenhof
3-Edge-Coloring Conjecture ★★★
Author(s): Arthur; Hoffmann-Ostenhof
Conjecture Suppose  with
with 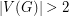 is a connected cubic graph admitting a
is a connected cubic graph admitting a  -edge coloring. Then there is an edge
-edge coloring. Then there is an edge 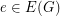 such that the cubic graph homeomorphic to
such that the cubic graph homeomorphic to 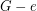 has a
has a  -edge coloring.
-edge coloring.
 with
with 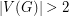 is a connected cubic graph admitting a
is a connected cubic graph admitting a  -edge coloring. Then there is an edge
-edge coloring. Then there is an edge 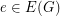 such that the cubic graph homeomorphic to
such that the cubic graph homeomorphic to 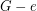 has a
has a  -edge coloring.
-edge coloring. Keywords: 3-edge coloring; 4-flow; removable edge
Cycle Double Covers Containing Predefined 2-Regular Subgraphs ★★★
Author(s): Arthur; Hoffmann-Ostenhof
Conjecture Let  be a
be a 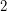 -connected cubic graph and let
-connected cubic graph and let  be a
be a 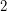 -regular subgraph such that
-regular subgraph such that 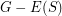 is connected. Then
is connected. Then  has a cycle double cover which contains
has a cycle double cover which contains  (i.e all cycles of
(i.e all cycles of  ).
).
 be a
be a 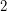 -connected cubic graph and let
-connected cubic graph and let  be a
be a 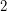 -regular subgraph such that
-regular subgraph such that 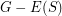 is connected. Then
is connected. Then  has a cycle double cover which contains
has a cycle double cover which contains  (i.e all cycles of
(i.e all cycles of  ).
). Keywords:
3-Decomposition Conjecture ★★★
Author(s): Arthur; Hoffmann-Ostenhof
Conjecture (3-Decomposition Conjecture) Every connected cubic graph  has a decomposition into a spanning tree, a family of cycles and a matching.
has a decomposition into a spanning tree, a family of cycles and a matching.
 has a decomposition into a spanning tree, a family of cycles and a matching.
has a decomposition into a spanning tree, a family of cycles and a matching. Keywords: cubic graph
Strong 5-cycle double cover conjecture ★★★
Author(s): Arthur; Hoffmann-Ostenhof
Conjecture Let  be a circuit in a bridgeless cubic graph
be a circuit in a bridgeless cubic graph  . Then there is a five cycle double cover of
. Then there is a five cycle double cover of  such that
such that  is a subgraph of one of these five cycles.
is a subgraph of one of these five cycles.
 be a circuit in a bridgeless cubic graph
be a circuit in a bridgeless cubic graph  . Then there is a five cycle double cover of
. Then there is a five cycle double cover of  such that
such that  is a subgraph of one of these five cycles.
is a subgraph of one of these five cycles. Keywords: cycle cover

 Drupal
Drupal CSI of Charles University
CSI of Charles University