 login/create account
login/create account
Conjecture Suppose  with
with 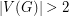 is a connected cubic graph admitting a
is a connected cubic graph admitting a  -edge coloring. Then there is an edge
-edge coloring. Then there is an edge 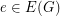 such that the cubic graph homeomorphic to
such that the cubic graph homeomorphic to 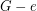 has a
has a  -edge coloring.
-edge coloring.
 with
with 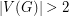 is a connected cubic graph admitting a
is a connected cubic graph admitting a  -edge coloring. Then there is an edge
-edge coloring. Then there is an edge 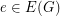 such that the cubic graph homeomorphic to
such that the cubic graph homeomorphic to 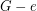 has a
has a  -edge coloring.
-edge coloring. Reformulation via 4-flows:
Conjecture Suppose  is a cubic graph with a nowhere-zero
is a cubic graph with a nowhere-zero 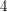 -flow, then there is an edge
-flow, then there is an edge 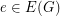 such that
such that 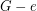 has a nowhere-zero
has a nowhere-zero 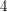 -flow.
-flow.
 is a cubic graph with a nowhere-zero
is a cubic graph with a nowhere-zero 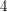 -flow, then there is an edge
-flow, then there is an edge 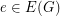 such that
such that 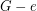 has a nowhere-zero
has a nowhere-zero 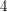 -flow.
-flow. Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University