 login/create account
login/create account
Beneš Conjecture ★★★
Author(s): Beneš
Let  be a non-empty finite set. Given a partition
be a non-empty finite set. Given a partition 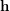 of
of  , the stabilizer of
, the stabilizer of 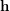 , denoted
, denoted 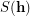 , is the group formed by all permutations of
, is the group formed by all permutations of  preserving each block of
preserving each block of 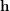 .
.
Problem ( ) Find a sufficient condition for a sequence of partitions
) Find a sufficient condition for a sequence of partitions 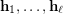 of
of  to be complete, i.e. such that the product of their stabilizers
to be complete, i.e. such that the product of their stabilizers 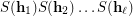 is equal to the whole symmetric group
is equal to the whole symmetric group 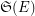 on
on  . In particular, what about completeness of the sequence
. In particular, what about completeness of the sequence 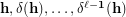 , given a partition
, given a partition 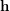 of
of  and a permutation
and a permutation  of
of  ?
?
 ) Find a sufficient condition for a sequence of partitions
) Find a sufficient condition for a sequence of partitions 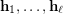 of
of  to be complete, i.e. such that the product of their stabilizers
to be complete, i.e. such that the product of their stabilizers 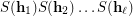 is equal to the whole symmetric group
is equal to the whole symmetric group 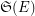 on
on  . In particular, what about completeness of the sequence
. In particular, what about completeness of the sequence 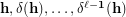 , given a partition
, given a partition 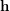 of
of  and a permutation
and a permutation  of
of  ?
? Conjecture (Beneš) Let 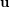 be a uniform partition of
be a uniform partition of  and
and 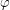 be a permutation of
be a permutation of  such that
such that 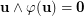 . Suppose that the set
. Suppose that the set 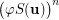 is transitive, for some integer
is transitive, for some integer 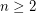 . Then
. Then 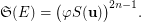
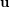 be a uniform partition of
be a uniform partition of  and
and 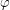 be a permutation of
be a permutation of  such that
such that 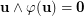 . Suppose that the set
. Suppose that the set 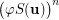 is transitive, for some integer
is transitive, for some integer 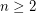 . Then
. Then 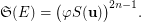
Keywords:
Chain-meet-closed sets ★★
Author(s): Porton
Let 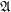 is a complete lattice. I will call a filter base a nonempty subset
is a complete lattice. I will call a filter base a nonempty subset  of
of 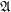 such that
such that 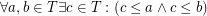 .
.
Definition A subset  of a complete lattice
of a complete lattice 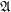 is chain-meet-closed iff for every non-empty chain
is chain-meet-closed iff for every non-empty chain 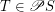 we have
we have 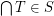 .
.
 of a complete lattice
of a complete lattice 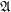 is chain-meet-closed iff for every non-empty chain
is chain-meet-closed iff for every non-empty chain 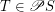 we have
we have 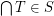 .
. Conjecture A subset  of a complete lattice
of a complete lattice 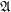 is chain-meet-closed iff for every filter base
is chain-meet-closed iff for every filter base 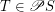 we have
we have 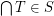 .
.
 of a complete lattice
of a complete lattice 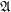 is chain-meet-closed iff for every filter base
is chain-meet-closed iff for every filter base 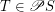 we have
we have 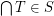 .
. Keywords: chain; complete lattice; filter bases; filters; linear order; total order

 Drupal
Drupal CSI of Charles University
CSI of Charles University