 login/create account
login/create account
Let 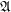 is a complete lattice. I will call a filter base a nonempty subset
is a complete lattice. I will call a filter base a nonempty subset  of
of 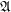 such that
such that 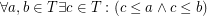 .
.
Definition A subset  of a complete lattice
of a complete lattice 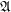 is chain-meet-closed iff for every non-empty chain
is chain-meet-closed iff for every non-empty chain 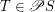 we have
we have 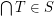 .
.
 of a complete lattice
of a complete lattice 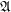 is chain-meet-closed iff for every non-empty chain
is chain-meet-closed iff for every non-empty chain 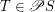 we have
we have 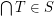 .
. Conjecture A subset  of a complete lattice
of a complete lattice 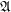 is chain-meet-closed iff for every filter base
is chain-meet-closed iff for every filter base 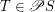 we have
we have 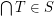 .
.
 of a complete lattice
of a complete lattice 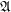 is chain-meet-closed iff for every filter base
is chain-meet-closed iff for every filter base 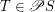 we have
we have 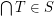 .
. The answer is yes. A proof is present in this online article.
Bibliography
*Victor Porton. Chain-meet-closed sets on complete lattices
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University