 login/create account
login/create account
Earth-Moon Problem ★★
Author(s): Ringel
Problem What is the maximum number of colours needed to colour countries such that no two countries sharing a common border have the same colour in the case where each country consists of one region on earth and one region on the moon ?
Keywords:
Triangle-packing vs triangle edge-transversal. ★★
Author(s): Tuza
Conjecture If  has at most
has at most  edge-disjoint triangles, then there is a set of
edge-disjoint triangles, then there is a set of 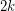 edges whose deletion destroys every triangle.
edges whose deletion destroys every triangle.
 has at most
has at most  edge-disjoint triangles, then there is a set of
edge-disjoint triangles, then there is a set of 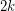 edges whose deletion destroys every triangle.
edges whose deletion destroys every triangle. Keywords:
Odd-cycle transversal in triangle-free graphs ★★
Author(s): Erdos; Faudree; Pach; Spencer
Conjecture If  is a simple triangle-free graph, then there is a set of at most
is a simple triangle-free graph, then there is a set of at most 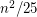 edges whose deletion destroys every odd cycle.
edges whose deletion destroys every odd cycle.
 is a simple triangle-free graph, then there is a set of at most
is a simple triangle-free graph, then there is a set of at most 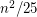 edges whose deletion destroys every odd cycle.
edges whose deletion destroys every odd cycle. Keywords:
Simultaneous partition of hypergraphs ★★
Problem Let 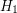 and
and 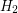 be two
be two  -uniform hypergraph on the same vertex set
-uniform hypergraph on the same vertex set 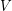 . Does there always exist a partition of
. Does there always exist a partition of 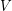 into
into  classes
classes  such that for both
such that for both 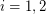 , at least
, at least 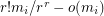 hyperedges of
hyperedges of 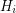 meet each of the classes
meet each of the classes  ?
?
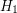 and
and 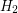 be two
be two  -uniform hypergraph on the same vertex set
-uniform hypergraph on the same vertex set 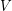 . Does there always exist a partition of
. Does there always exist a partition of 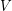 into
into  classes
classes  such that for both
such that for both 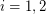 , at least
, at least 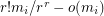 hyperedges of
hyperedges of  meet each of the classes
meet each of the classes  ?
? Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University