 login/create account
login/create account
 has at most
has at most  edge-disjoint triangles, then there is a set of
edge-disjoint triangles, then there is a set of 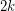 edges whose deletion destroys every triangle.
edges whose deletion destroys every triangle. This conjecture may be rephrased in terms of packing and edge-transversal. A triangle packing is a set of pairwise edge-disjoint triangles. A triangle edge-tranversal is a set of edges meeting all triangles. Denote the maximum size of a triangle packing in  by
by 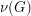 and the minimum size of a triangle edge-transversal of
and the minimum size of a triangle edge-transversal of  by
by 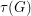 . Clearly
. Clearly 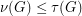 . The conjecture translates in
. The conjecture translates in 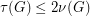 .
.
This conjecture, if true, is best possible as can be seen by taking, say 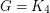 or
or 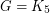 . Trivially,
. Trivially, 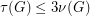 , since the set of edges of a maximum triangle packing is a triangle edge-transversal. Haxell [H] proved that
, since the set of edges of a maximum triangle packing is a triangle edge-transversal. Haxell [H] proved that 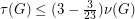 edges whose deletion destroys every triangle.
edges whose deletion destroys every triangle.
As usual, one can define fractional packing and fractional transversal. Let 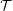 be the set of triangles of
be the set of triangles of  . A fractional triangle packing is a function
. A fractional triangle packing is a function 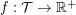 such that
such that 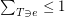 for every edge
for every edge  . A fractional triangle edge-transversal is a function
. A fractional triangle edge-transversal is a function 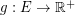 such that
such that 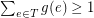 for every triangle
for every triangle 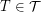 . We denote by
. We denote by 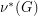 the maximum of
the maximum of 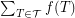 over all fractional triangle packing and by
over all fractional triangle packing and by 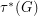 the minimum of
the minimum of 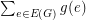 over all fractional edge-transversals. By duality of linear programming
over all fractional edge-transversals. By duality of linear programming 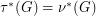 . Krivelevich [K] proved two fractional versions of the conjecture:
. Krivelevich [K] proved two fractional versions of the conjecture:
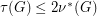 and
and 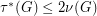 .
.
Bibliography
[H] P.Haxell, Packing and covering triangles in graphs, Discrete Mathematics 195 (1999), no. 1–3, 251–254.
[K] M. Krivelevich, On a conjecture of Tuza about packing and covering of triangles Discrete Mathematics 142 (1995), 281-286.
*[T] Z. Tuza, A conjecture on triangles of graphs. Graphs Combin. 6 (1990), 373-380.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University