 login/create account
login/create account
Earth-Moon Problem
In term of graphs, it can be rephrased as follows. What is the maximum chromatic number of a graph  which is the union of two planar graphs (on the same vertex set)?
which is the union of two planar graphs (on the same vertex set)?
If a graph  on
on  vertices is the union of two planar graphs, then it has at most
vertices is the union of two planar graphs, then it has at most 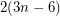 edges, and so it is has a vertex of degree at most
edges, and so it is has a vertex of degree at most  . An easy induction shows that
. An easy induction shows that  is 12-colourable, as observed by Heawood [He]. Gardner [G] reported an example requiring 9 colours (the join of
is 12-colourable, as observed by Heawood [He]. Gardner [G] reported an example requiring 9 colours (the join of 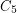 and
and 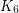 ). It is not known if configurations exist requiring 10, 11, or 12 colours.
). It is not known if configurations exist requiring 10, 11, or 12 colours.
More generally, one may ask for the maximum chromatic number of the union of  planar graphs.
planar graphs.
 which is the union of
which is the union of  planar graphs?
planar graphs? The same reasoning as above shows that 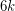 colours are always sufficient. The minimum number of planar graphs to decompose a complete graph [BW] gives a lower bound of
colours are always sufficient. The minimum number of planar graphs to decompose a complete graph [BW] gives a lower bound of 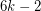 for
for 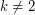 .
.
Bibliography
[BW] L. W. Beineke and A. T. White, Topological Graph Theory, Selected Topics in Graph Theory, L. W. Beineke and R. J. Wilson, eds., Academic Press, 15-50, 1978.
[G] M. Gardner, Mathematical Recreations: The Coloring of Unusual Maps Leads Into Uncharted Territory. Sci. Amer. 242, 14-22, 1980.
[He] P.J. Heawood, Map Colour Theorems. Quart. J. Pure Appl. Math. 24, 332-338, 1890.
*[R] G. Ringel, Färbungsprobleme auf Flachen und Graphen. Berlin: Deutsche Verlag der Wissenschaften, 1959.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University