 login/create account
login/create account
Kriesell's Conjecture ★★
Author(s): Kriesell
Conjecture Let  be a graph and let
be a graph and let 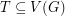 such that for any pair
such that for any pair 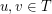 there are
there are 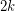 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains  edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains  .
.
 be a graph and let
be a graph and let 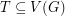 such that for any pair
such that for any pair 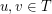 there are
there are 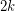 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains  edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains  .
. Keywords: Disjoint paths; edge-connectivity; spanning trees
2-colouring a graph without a monochromatic maximum clique ★★
Conjecture If  is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a  -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic.
 is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a  -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic. Keywords: maximum clique; Partitioning
Distributivity of a lattice of funcoids is not provable without axiom of choice ★
Author(s): Porton
Conjecture Distributivity of the lattice 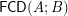 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets  and
and 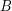 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice).
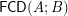 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets  and
and 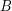 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice). A similar conjecture:
Conjecture 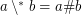 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice).
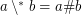 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice). Keywords: axiom of choice; distributive lattice; distributivity; funcoid; reverse math; reverse mathematics; ZF; ZFC

 Drupal
Drupal CSI of Charles University
CSI of Charles University