 login/create account
login/create account
Problem Consider the set of all topologically inequivalent polyhedra with  edges. Define a form parameter for a polyhedron as
edges. Define a form parameter for a polyhedron as 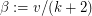 where
where  is the number of vertices. What is the distribution of
is the number of vertices. What is the distribution of 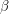 for
for 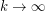 ?
?
 edges. Define a form parameter for a polyhedron as
edges. Define a form parameter for a polyhedron as 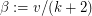 where
where  is the number of vertices. What is the distribution of
is the number of vertices. What is the distribution of 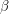 for
for 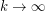 ?
? Consider the set of all topologically inequivalent polyhedra on a sphere with k edges (i.e. polyhedral graphs, Sloan Sequence A002840 ). Due to duality the distribution of the form parameter 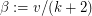 is symmetric about
is symmetric about 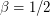 . Now a natural question is whether the distribution of beta tends to a limiting distribution when the number of edges tends to infinity. Is there any nontrivial limit theorem by means of rescaling? Some numerical values can be found on Counting Polyhedra suggesting that the distribution concentrates around
. Now a natural question is whether the distribution of beta tends to a limiting distribution when the number of edges tends to infinity. Is there any nontrivial limit theorem by means of rescaling? Some numerical values can be found on Counting Polyhedra suggesting that the distribution concentrates around 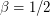 .
.

 Drupal
Drupal CSI of Charles University
CSI of Charles University