 login/create account
login/create account
polyhedral graphs, distribution
Asymptotic Distribution of Form of Polyhedra ★★
Author(s): Rüdinger
Problem Consider the set of all topologically inequivalent polyhedra with  edges. Define a form parameter for a polyhedron as
edges. Define a form parameter for a polyhedron as 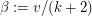 where
where  is the number of vertices. What is the distribution of
is the number of vertices. What is the distribution of 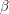 for
for 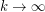 ?
?
 edges. Define a form parameter for a polyhedron as
edges. Define a form parameter for a polyhedron as 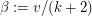 where
where  is the number of vertices. What is the distribution of
is the number of vertices. What is the distribution of 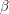 for
for 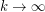 ?
? Keywords: polyhedral graphs, distribution

 Drupal
Drupal CSI of Charles University
CSI of Charles University