 login/create account
login/create account
Conjecture Let  be an abelian group. Is the core of a Cayley graph (on some power of
be an abelian group. Is the core of a Cayley graph (on some power of  ) a Cayley graph (on some power of
) a Cayley graph (on some power of  )?
)?
 be an abelian group. Is the core of a Cayley graph (on some power of
be an abelian group. Is the core of a Cayley graph (on some power of  ) a Cayley graph (on some power of
) a Cayley graph (on some power of  )?
)? Even the case 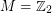 is open. In this case, Cayley graphs on some power of
is open. In this case, Cayley graphs on some power of 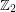 are called cube-like graphs, they have been introduced by Lov\'asz as an example of graphs, for which every eigenvalue is an integer.
are called cube-like graphs, they have been introduced by Lov\'asz as an example of graphs, for which every eigenvalue is an integer.
So, in this case we ask, whether a core of each cube-like graph is a cube-like graph.

 Drupal
Drupal CSI of Charles University
CSI of Charles University