Home » Subject » Analysis

pushing Bertrand series (Solved)

Importance: Low ✭
Author(s):
Subject: Analysis
Keywords:
Recomm. for undergrads: no
Posted by: Jerome JEAN-CHARLES
on: May 20th, 2009
Solved by:
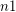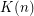Question   Definitions: For $ n \gt 1 $ : Let $ K(n) $ be the last 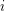$ i $ such that the i'th iteration of log composition on $ n $ is still above 1.

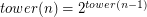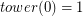Remark: K(n) is the "towerian log" where $ tower(n) = 2^{tower(n-1)} $ and $ tower(0)=1 $.

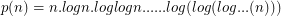Let $ p(n) = n.logn.loglogn......log(log(log... (n))) $ where the last log is iterated 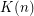$ K(n) $ times.

PROBLEM : Is 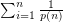$ \sum_{i=1}^{n} \frac{1}{p(n)} $. convergent or divergent.

REMARKS: The log could be in base 2 this clearly does not affect the result.

The log could be replaced by ceil(log) or floor(log) , this may affect the result.

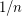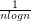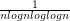MOTIVATION: the sum of $ 1/n $ ( harmonic serie is divergent) , the same is true with $ \frac{1}{nlogn} $ and $ \frac{1}{nlognloglogn} $ etc (called bertrand series I think) .

HISTORY: I made it up, it should have been thought of somewhere else (my culture in analysis is small).


add new comment

Status

On May 20th, 2009 Robert Samal says:

I'm changing this to Solved and to a "not serious research" category. (Very nice exercise, though!)

reply

This is a Putnam problem

On May 20th, 2009 Anonymous says:

And a recent one at that. 2008 A4 and FYI it diverges by what is sometimes called the integral test.

reply

Solution

On May 20th, 2009 Anonymous says:

appears e.g. on http://www.mathlinks.ro/Forum/viewtopic.php?t=244046

reply

Jérôme JEAN-CHARLES start

On May 20th, 2009 Jerome JEAN-CHARLES says:

Jérôme JEAN-CHARLES start is n > 1 . For motivation you get convergence as soon as you square the last log term in Bertrand series like 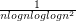$ \frac{1}{nlognloglogn^2} $.

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.