 login/create account
login/create account
Question Definitions: For 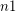 : Let
: Let 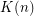 be the last
be the last 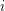 such that the i'th iteration of log composition on
such that the i'th iteration of log composition on  is still above 1.
is still above 1.
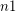 : Let
: Let 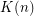 be the last
be the last 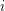 such that the i'th iteration of log composition on
such that the i'th iteration of log composition on  is still above 1.
is still above 1.
Remark: K(n) is the "towerian log" where 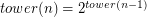 and
and 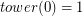 .
.
Let 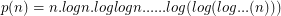 where the last log is iterated
where the last log is iterated 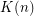 times.
times.
PROBLEM : Is 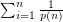 . convergent or divergent.
. convergent or divergent.
REMARKS: The log could be in base 2 this clearly does not affect the result.
The log could be replaced by ceil(log) or floor(log) , this may affect the result.
MOTIVATION: the sum of 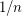 ( harmonic serie is divergent) , the same is true with
( harmonic serie is divergent) , the same is true with 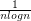 and
and 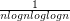 etc (called bertrand series I think) .
etc (called bertrand series I think) .
HISTORY: I made it up, it should have been thought of somewhere else (my culture in analysis is small).

 Drupal
Drupal CSI of Charles University
CSI of Charles University