 login/create account
login/create account
Partial List Coloring
Let  be a simple graph, and for every list assignment
be a simple graph, and for every list assignment 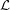 let
let 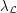 be the maximum number of vertices of
be the maximum number of vertices of  which are colorable with respect to
which are colorable with respect to 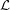 . Define
. Define  , where the minimum is taken over all list assignments
, where the minimum is taken over all list assignments 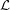 with
with 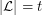 for all
for all 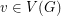 .
.
Conjecture [2] Let  be a graph with list chromatic number
be a graph with list chromatic number 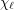 and
and 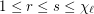 . Then
. Then ![\[\frac{\lambda_r}{r}\geq\frac{\lambda_s}{s}.\]](/files/tex/47be18e956355dd433b88b66eabf01a9e3ed5f61.png)
 be a graph with list chromatic number
be a graph with list chromatic number 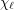 and
and 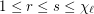 . Then
. Then ![\[\frac{\lambda_r}{r}\geq\frac{\lambda_s}{s}.\]](/files/tex/47be18e956355dd433b88b66eabf01a9e3ed5f61.png)
As you see this conjecture in the special case 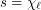 , is the conjecture of Albertson, Grossman and Haas [1]:
, is the conjecture of Albertson, Grossman and Haas [1]: 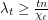 for any
for any 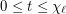 .
.
Bibliography
[1] M. Albertson, S. Grossman and R. Haas, Partial list colouring, Discrete Math., 214(2000), pp. 235-240.
[2] Moharram N. Iradmusa, A Note on Partial List Colorings, Australasian Journal of Combinatorics, Vol.46, 2010,  .
.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University