 login/create account
login/create account
Inequality of complex numbers (Solved)
Conjecture There exists a real positive  , such that for any
, such that for any 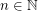 and any
and any 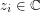 where
where 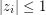 for
for 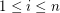 and
and 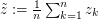 , the following holds:
, the following holds: 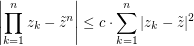
 , such that for any
, such that for any 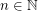 and any
and any 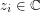 where
where 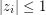 for
for 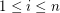 and
and 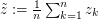 , the following holds:
, the following holds: 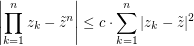
Bibliography
* indicates original appearance(s) of problem.
A hint: \par Let with
On July 29th, 2010 Anonymous says:
A hint: \par Let 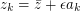 with
with  small and
small and 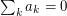 . Then
. Then 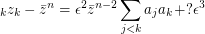 and
and 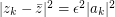 . \par Now from
. \par Now from 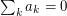 it follows that
it follows that 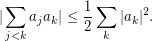 This shows that your inequality has ``the right order of magnitude'' with
This shows that your inequality has ``the right order of magnitude'' with 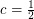 .
.
A hint
On August 1st, 2010 Christian Blatter says:
I am the author of this hint and somehow mismanaged the posting. So here it is again:
Let 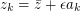 with
with  small and
small and 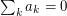 . Then
. Then 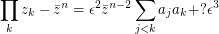 and
and 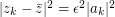 .
.
Now from 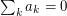 it follows that
it follows that 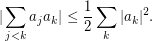 This shows that your inequality has the "right order of magnitude" with
This shows that your inequality has the "right order of magnitude" with 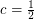 .
.
Requesting background information
On April 21st, 2010 Carolus says:
To feanor, the author of this conjecture:
What is the motivation for this conjecture ? The selected importance "medium" let me assume the verification or falsification of this conjecture would bring some benefit. If possible, describe that benefit ("practical" applications or consequences), please.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Yes, such exists, say
Yes, such exists, say
exists, say 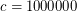 works. Assume the contrary and consider the counterexample. Without loss of generality,
works. Assume the contrary and consider the counterexample. Without loss of generality, 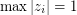 , else multiple all
, else multiple all 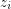 's to some
's to some 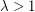 so that this bacomes true, LHS is multiplied by
so that this bacomes true, LHS is multiplied by 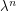 , while RHS only by
, while RHS only by 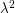 . So, we again get a counterexample. Denote
. So, we again get a counterexample. Denote 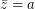 ,
, 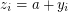 ,
, 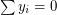 . Since LHS does not exceed 2, we have
. Since LHS does not exceed 2, we have 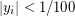 (else RHS is too large). Hence
(else RHS is too large). Hence 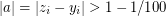 for
for 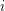 s.t.
s.t. 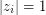 . Then we have
. Then we have 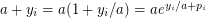 , where
, where 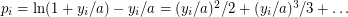 ,
, 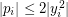 by some easy estimate. Finally, LHS equals
by some easy estimate. Finally, LHS equals 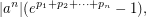 and we just use estimate
and we just use estimate 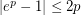 for small enough
for small enough 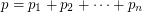 (
( is small enough, since
is small enough, since 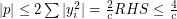 ).
).