 login/create account
login/create account
Conjecture There exists a real positive  , such that for any
, such that for any 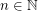 and any
and any 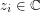 where
where 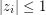 for
for 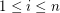 and
and 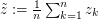 , the following holds:
, the following holds: 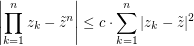
 , such that for any
, such that for any 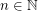 and any
and any 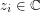 where
where 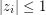 for
for 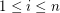 and
and 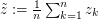 , the following holds:
, the following holds: 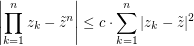
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University