 login/create account
login/create account
Geodesic cycles and Tutte's Theorem
Problem If  is a
is a  -connected finite graph, is there an assignment of lengths
-connected finite graph, is there an assignment of lengths 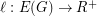 to the edges of
to the edges of  , such that every
, such that every  -geodesic cycle is peripheral?
-geodesic cycle is peripheral?
 is a
is a  -connected finite graph, is there an assignment of lengths
-connected finite graph, is there an assignment of lengths 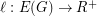 to the edges of
to the edges of  , such that every
, such that every  -geodesic cycle is peripheral?
-geodesic cycle is peripheral? A cycle  is
is  -geodesic if for every two vertices
-geodesic if for every two vertices 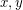 on
on  there is no
there is no  -
-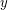 ~path in
~path in  shorter, with respect to
shorter, with respect to  , than both
, than both  -
-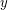 ~arcs on
~arcs on  .
.
It is not hard to prove [GS] that for every finite graph  and every assignment of edge lengths
and every assignment of edge lengths 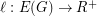 the
the  -geodesic cycles of
-geodesic cycles of  generate its cycle space. Thus, a positive answer to the problem would imply a new proof of Tutte's classical theorem [T] that the peripheral cycles of a
generate its cycle space. Thus, a positive answer to the problem would imply a new proof of Tutte's classical theorem [T] that the peripheral cycles of a  -connected finite graph generate its cycle space.
-connected finite graph generate its cycle space.
Bibliography
*[GS] Angelos Georgakopoulos, Philipp Sprüssel: Geodesic topological cycles in locally finite graphs. Preprint 2007.
[T] W.T. Tutte, How to draw a graph. Proc. London Math. Soc. 13 (1963), 743–768.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University