 login/create account
login/create account
Sprüssel, Philipp
Geodesic cycles and Tutte's Theorem ★★
Author(s): Georgakopoulos; Sprüssel
Problem If  is a
is a  -connected finite graph, is there an assignment of lengths
-connected finite graph, is there an assignment of lengths 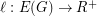 to the edges of
to the edges of  , such that every
, such that every  -geodesic cycle is peripheral?
-geodesic cycle is peripheral?
 is a
is a  -connected finite graph, is there an assignment of lengths
-connected finite graph, is there an assignment of lengths 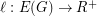 to the edges of
to the edges of  , such that every
, such that every  -geodesic cycle is peripheral?
-geodesic cycle is peripheral? Keywords: cycle space; geodesic cycles; peripheral cycles

 Drupal
Drupal CSI of Charles University
CSI of Charles University