Home » Subject » Combinatorics » Matroid Theory

Equality in a matroidal circumference bound

Importance: Medium ✭✭
Author(s): Oxley, James
Royle, Gordon
Subject: Combinatorics
» Matroid Theory
Keywords: circumference
Recomm. for undergrads: no
Posted by: Gordon Royle
on: November 2nd, 2007
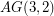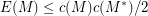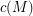Question   Is the binary affine cube $ AG(3,2) $ the only 3-connected matroid for which equality holds in the bound $$E(M) \leq c(M) c(M^*) / 2$$ where $ c(M) $ is the circumference (i.e. largest circuit size) of $ M $?

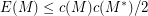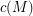If $ M $ is a 2-connected matroid with at least two elements then it was proved in [LO] that $$ E(M) \leq c(M) c(M^*) / 2 $$ where $ c(M) $ is the size of the largest circuit in $ M $.

Equality can hold in this bound -- in particular the binary affine cube 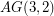$ AG(3,2) $ is an 8-element self-dual matroid with circumference 4. There are various graphic matroids for which equality holds, and these have been classified in [W] where it is shown that they are all series-parallel networks and hence not 3-connected.

This question is therefore asking whether 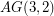$ AG(3,2) $ is the sole $ 3 $-connected example where equality holds; this is known to be true for all matroids on up to 9 elements.

(A variant of this question would be to ask if 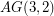$ AG(3,2) $ is the only non-graphic example other than trivial modifications like replacing every element with an equally sized parallel class.)

Bibliography

[LO] Lemos, Manoel; Oxley, James A sharp bound on the size of a connected matroid. Trans. Amer. Math. Soc. 353 (2001), no. 10, 4039--4056 MathSciNet

[W] Wu, Pou-Lin Extremal graphs with prescribed circumference and cocircumference. Discrete Math. 223 (2000), no. 1-3, 299--308 MathSciNet


* indicates original appearance(s) of problem.
add new comment