Open Problem Garden

Importance: Medium ✭✭

Author(s):	Oxley, James
	Royle, Gordon

Subject:	Combinatorics
	» Matroid Theory

Keywords:

circumference

Recomm. for undergrads: no

Posted	by:	Gordon Royle
	on:	November 2nd, 2007

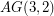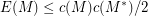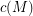Question Is the binary affine cube $AG(3,2)$ the only 3-connected matroid for which equality holds in the bound $E(M) \leq c(M) c(M^*) / 2$ where $c(M)$ is the circumference (i.e. largest circuit size) of $M$ ?

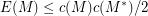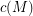If $M$ is a 2-connected matroid with at least two elements then it was proved in [LO] that $E(M) \leq c(M) c(M^*) / 2$ where $c(M)$ is the size of the largest circuit in $M$ .

Equality can hold in this bound -- in particular the binary affine cube 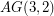$AG(3,2)$ is an 8-element self-dual matroid with circumference 4. There are various graphic matroids for which equality holds, and these have been classified in [W] where it is shown that they are all series-parallel networks and hence not 3-connected.

This question is therefore asking whether 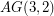$AG(3,2)$ is the sole $3$ -connected example where equality holds; this is known to be true for all matroids on up to 9 elements.

(A variant of this question would be to ask if 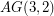$AG(3,2)$ is the only non-graphic example other than trivial modifications like replacing every element with an equally sized parallel class.)

Bibliography

[LO] Lemos, Manoel; Oxley, James A sharp bound on the size of a connected matroid. Trans. Amer. Math. Soc. 353 (2001), no. 10, 4039--4056 MathSciNet

[W] Wu, Pou-Lin Extremal graphs with prescribed circumference and cocircumference. Discrete Math. 223 (2000), no. 1-3, 299--308 MathSciNet

* indicates original appearance(s) of problem.

add new comment

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity