 login/create account
login/create account
Hamilton decomposition of prisms over 3-connected cubic planar graphs
Conjecture Every prism over a  -connected cubic planar graph can be decomposed into two Hamilton cycles.
-connected cubic planar graph can be decomposed into two Hamilton cycles.
 -connected cubic planar graph can be decomposed into two Hamilton cycles.
-connected cubic planar graph can be decomposed into two Hamilton cycles. The prism over a graph  is the Cartesian product
is the Cartesian product 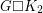 .
.
Rosenfeld and Barnette [RB] deduced from the Four-Colour Theorem that the prism over cubic planar 3-connected  has a Hamilton cycle
has a Hamilton cycle  . The graph
. The graph 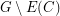 is cycle factor (spanning union of cycles). The conjecture says that one can choses
is cycle factor (spanning union of cycles). The conjecture says that one can choses  so that the cycle factor
so that the cycle factor 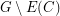 has a unique cycle, that is a Hamilton cycle.
has a unique cycle, that is a Hamilton cycle.
Bibliography
*[AR] B. Alspach and M. Rosenfeld, On Hamilton decompositions of prisms over simple  -polytopes. Graphs Combin. 2 (1986), 1--8.
-polytopes. Graphs Combin. 2 (1986), 1--8.
[RB] M. Rosenfeld and D. Barnette, Hamiltonian circuits in certain prisms, Discrete Math. 5 (1973) 389–394.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University