 login/create account
login/create account
Cycles in Graphs of Large Chromatic Number
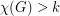 , then
, then  contains at least
contains at least 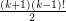 cycles of length
cycles of length 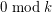 .
.
Chudnovsky, Plumettaz, Scott and Seymour [CPSS] proved that every graph with chromatic number at least 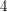 contains a cycle of length
contains a cycle of length 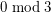 . A simpler proof was found by Wrochna [W]. Wrochna's argument was generalised by Brewster, McGuinness, Moore and Noel [BMMN] to the following: if
. A simpler proof was found by Wrochna [W]. Wrochna's argument was generalised by Brewster, McGuinness, Moore and Noel [BMMN] to the following: if 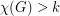 , then
, then  contains at least TeX Embedding failed! cycles of length
contains at least TeX Embedding failed! cycles of length 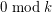 .} The compete graph on
.} The compete graph on 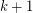 vertices has exactly
vertices has exactly 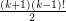 cycles of length
cycles of length 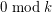 and so the conjecture above, if true, would be best possible.
and so the conjecture above, if true, would be best possible.
Bibliography
[BMMN] R. C. Brewster, S. McGuinness, B. Moore, J. A. Noel, A Dichotomy Theorem for Circular Colouring Reconfiguration, submitted, arXiv:1508.05573v1.
[CPSS] M. Chudnovsky, M. Plumettaz, A. Scott, and P. Seymour, The Structure of Graphs with no Cycles of Length Divisible by Three, in preparation.
[Wro] M. Wrochna, unpublished.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University