 login/create account
login/create account
Co-separability of filter objects (Solved)
 and
and  are filters on a set
are filters on a set 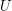 and
and 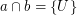 . Then
. Then 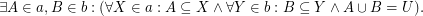
See here for some equivalent reformulations of this problem.
This problem (in fact, a little more general version of a problem equivalent to this problem) was solved by the problem author. See here for the solution.
Maybe this problem should be moved to "second-tier" because its solution is simple.
Bibliography
*Victor Porton. Open problem: co-separability of filter objects
* indicates original appearance(s) of problem.
Your example is wrong
The set of all infinite sets of integers is not a filter. For example 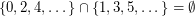 .
.
I haven't read your comment further.
Correction
Sorry, I was too hasty. What I meant is that  is a "nontrivial ultrafilter" (wikipedia page ultrafilter) calls this "non-principal ultrafilter".
is a "nontrivial ultrafilter" (wikipedia page ultrafilter) calls this "non-principal ultrafilter".
No counterexamples, it is proved
Then take 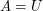 and
and 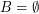 (I do not require filters to be proper).
(I do not require filters to be proper).
Robert, why you are trying to find a counter-example for a proved theorem?
--
Victor Porton - http://www.mathematics21.org
Is it really?
You require that 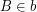 , and my filter
, and my filter  does not contain empty set. I'm trying to find a counter-example because either I misunderstand the statement of the theorem, or the theorem is false.
does not contain empty set. I'm trying to find a counter-example because either I misunderstand the statement of the theorem, or the theorem is false.
Some proofs just happen to have mistakes. Unfortunately, I don't understand yours, it apparently uses lot of notation (up, down, Cor, ...) that I'm unfamiliar with.
Oh, my mistake
I made a mistake in the statement of the conjecture as published on OPG. I corrected the problem statement both on OPG and on my blog. It should be 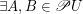 rather than
rather than 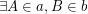 .
.
Indeed the equivalent reformulations of the theorem are correct and my proof (of a more general statement than this theorem) is not affected by the above mentioned error.
Robert, you do not understand me because I introduced new notations (that up, down, Cor, etc.) You may wish to read my preprint about these things (filters on posets and generalizations).

 Drupal
Drupal CSI of Charles University
CSI of Charles University
A counterexample?
From the link it seems you have proved the result. What about the following what seems to be a counterexample?
Now there is no set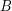 that would be minimal in
that would be minimal in  ...
...