 login/create account
login/create account
Conjecture Let  and
and  are filters on a set
are filters on a set 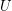 and
and 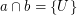 . Then
. Then 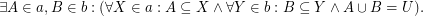
 and
and  are filters on a set
are filters on a set 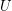 and
and 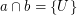 . Then
. Then 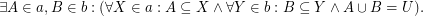
See here for some equivalent reformulations of this problem.
This problem (in fact, a little more general version of a problem equivalent to this problem) was solved by the problem author. See here for the solution.
Maybe this problem should be moved to "second-tier" because its solution is simple.
Bibliography
*Victor Porton. Open problem: co-separability of filter objects
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University