 login/create account
login/create account
Outward reloid of composition vs composition of outward reloids ★★
Author(s): Porton
Conjecture For every composable funcoids  and
and 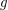
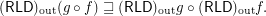
 and
and 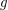
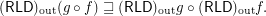
Keywords: outward reloid
A funcoid related to directed topological spaces ★★
Author(s): Porton
Conjecture Let 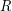 be the complete funcoid corresponding to the usual topology on extended real line
be the complete funcoid corresponding to the usual topology on extended real line ![$ [-\infty,+\infty] = \mathbb{R}\cup\{-\infty,+\infty\} $](/files/tex/3252019c60a83f00ff396d823dbff8040639f409.png) . Let
. Let 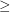 be the order on this set. Then
be the order on this set. Then 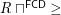 is a complete funcoid.
is a complete funcoid.
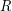 be the complete funcoid corresponding to the usual topology on extended real line
be the complete funcoid corresponding to the usual topology on extended real line ![$ [-\infty,+\infty] = \mathbb{R}\cup\{-\infty,+\infty\} $](/files/tex/3252019c60a83f00ff396d823dbff8040639f409.png) . Let
. Let 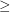 be the order on this set. Then
be the order on this set. Then 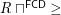 is a complete funcoid.
is a complete funcoid. Proposition It is easy to prove that 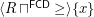 is the infinitely small right neighborhood filter of point
is the infinitely small right neighborhood filter of point ![$ x\in[-\infty,+\infty] $](/files/tex/4e57a21194d8d5a659e259a111ed13a9c23b52a1.png) .
.
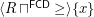 is the infinitely small right neighborhood filter of point
is the infinitely small right neighborhood filter of point ![$ x\in[-\infty,+\infty] $](/files/tex/4e57a21194d8d5a659e259a111ed13a9c23b52a1.png) .
. If proved true, the conjecture then can be generalized to a wider class of posets.
Keywords:
Infinite distributivity of meet over join for a principal funcoid ★★
Author(s): Porton
Conjecture 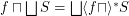 for principal funcoid
for principal funcoid  and a set
and a set 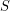 of funcoids of appropriate sources and destinations.
of funcoids of appropriate sources and destinations.
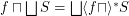 for principal funcoid
for principal funcoid  and a set
and a set 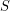 of funcoids of appropriate sources and destinations.
of funcoids of appropriate sources and destinations. Keywords: distributivity; principal funcoid
Entourages of a composition of funcoids ★★
Author(s): Porton
Conjecture 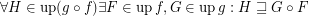 for every composable funcoids
for every composable funcoids  and
and 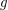 .
.
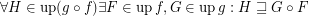 for every composable funcoids
for every composable funcoids  and
and 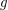 .
. Keywords: composition of funcoids; funcoids
Weak saturation of the cube in the clique ★
Problem
Determine 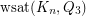 .
.
Keywords: bootstrap percolation; hypercube; Weak saturation

 Drupal
Drupal CSI of Charles University
CSI of Charles University