 login/create account
login/create account
Conjecture Let 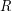 be the complete funcoid corresponding to the usual topology on extended real line
be the complete funcoid corresponding to the usual topology on extended real line ![$ [-\infty,+\infty] = \mathbb{R}\cup\{-\infty,+\infty\} $](/files/tex/3252019c60a83f00ff396d823dbff8040639f409.png) . Let
. Let 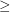 be the order on this set. Then
be the order on this set. Then 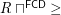 is a complete funcoid.
is a complete funcoid.
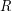 be the complete funcoid corresponding to the usual topology on extended real line
be the complete funcoid corresponding to the usual topology on extended real line ![$ [-\infty,+\infty] = \mathbb{R}\cup\{-\infty,+\infty\} $](/files/tex/3252019c60a83f00ff396d823dbff8040639f409.png) . Let
. Let 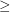 be the order on this set. Then
be the order on this set. Then 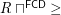 is a complete funcoid.
is a complete funcoid. Proposition It is easy to prove that 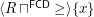 is the infinitely small right neighborhood filter of point
is the infinitely small right neighborhood filter of point ![$ x\in[-\infty,+\infty] $](/files/tex/4e57a21194d8d5a659e259a111ed13a9c23b52a1.png) .
.
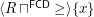 is the infinitely small right neighborhood filter of point
is the infinitely small right neighborhood filter of point ![$ x\in[-\infty,+\infty] $](/files/tex/4e57a21194d8d5a659e259a111ed13a9c23b52a1.png) .
. If proved true, the conjecture then can be generalized to a wider class of posets.
See Algebraic General Topology for definitions of used concepts.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University