 login/create account
login/create account
Problem
Determine 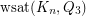 .
.
Given graphs  and
and  , let
, let 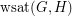 denote the minimum number of edges in a subgraph
denote the minimum number of edges in a subgraph 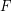 of
of  such that the edges of
such that the edges of 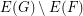 can be added to
can be added to 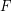 , one edge at a time, so that each edge completes a copy of
, one edge at a time, so that each edge completes a copy of  when it is added.
when it is added.
Of course, if one can solve the problem above, then a natural next step is to determine 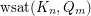 for all
for all  and
and  .
.
Morrison, Noel and Scott [MNS] solved the related problem of determining 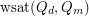 for all
for all  and
and  .
.
Bibliography
[MNS] N. Morrison, J. A. Noel, A. Scott. Saturation in the hypercube and bootstrap percolation. To appear in Combin. Probab. Comput.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University