 login/create account
login/create account
Odd cycles and low oddness ★★
Author(s):
Conjecture If in a bridgeless cubic graph  the cycles of any
the cycles of any  -factor are odd, then
-factor are odd, then 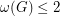 , where
, where 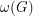 denotes the oddness of the graph
denotes the oddness of the graph  , that is, the minimum number of odd cycles in a
, that is, the minimum number of odd cycles in a  -factor of
-factor of  .
.
 the cycles of any
the cycles of any  -factor are odd, then
-factor are odd, then 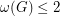 , where
, where 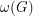 denotes the oddness of the graph
denotes the oddness of the graph  , that is, the minimum number of odd cycles in a
, that is, the minimum number of odd cycles in a  -factor of
-factor of  .
. Keywords:
Beneš Conjecture ★★★
Author(s): Beneš
Let  be a non-empty finite set. Given a partition
be a non-empty finite set. Given a partition 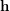 of
of  , the stabilizer of
, the stabilizer of 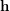 , denoted
, denoted 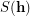 , is the group formed by all permutations of
, is the group formed by all permutations of  preserving each block of
preserving each block of 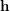 .
.
Problem ( ) Find a sufficient condition for a sequence of partitions
) Find a sufficient condition for a sequence of partitions 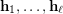 of
of  to be complete, i.e. such that the product of their stabilizers
to be complete, i.e. such that the product of their stabilizers 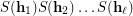 is equal to the whole symmetric group
is equal to the whole symmetric group 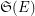 on
on  . In particular, what about completeness of the sequence
. In particular, what about completeness of the sequence 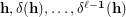 , given a partition
, given a partition 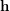 of
of  and a permutation
and a permutation  of
of  ?
?
 ) Find a sufficient condition for a sequence of partitions
) Find a sufficient condition for a sequence of partitions 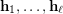 of
of  to be complete, i.e. such that the product of their stabilizers
to be complete, i.e. such that the product of their stabilizers 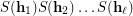 is equal to the whole symmetric group
is equal to the whole symmetric group 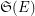 on
on  . In particular, what about completeness of the sequence
. In particular, what about completeness of the sequence 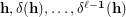 , given a partition
, given a partition 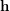 of
of  and a permutation
and a permutation  of
of  ?
? Conjecture (Beneš) Let 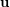 be a uniform partition of
be a uniform partition of  and
and 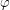 be a permutation of
be a permutation of  such that
such that 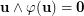 . Suppose that the set
. Suppose that the set 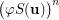 is transitive, for some integer
is transitive, for some integer 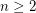 . Then
. Then 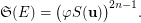
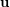 be a uniform partition of
be a uniform partition of  and
and 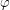 be a permutation of
be a permutation of  such that
such that 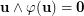 . Suppose that the set
. Suppose that the set 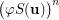 is transitive, for some integer
is transitive, for some integer 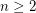 . Then
. Then 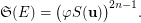
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University