 login/create account
login/create account
A cubic graph  is
is  -edge-colorable for a Steiner triple system
-edge-colorable for a Steiner triple system  if its edges can be colored with the points of
if its edges can be colored with the points of  in such a way that the points assigned to three edges sharing a vertex form a triple in
in such a way that the points assigned to three edges sharing a vertex form a triple in  .
.
A Steiner triple system  is called universal if any (simple) cubic graph is
is called universal if any (simple) cubic graph is  -colorable.
-colorable.
It is easy to see that if 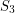 denotes the trivial Steiner triple system with three points and one triple, then
denotes the trivial Steiner triple system with three points and one triple, then 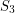 -colorable graphs are precisely (cubic) edge-3-colorable graphs. For the same reason, any cubic edge-3-colorable graph is
-colorable graphs are precisely (cubic) edge-3-colorable graphs. For the same reason, any cubic edge-3-colorable graph is  -colorable for any Steiner triple system (with at least one edge). Thus, the study of
-colorable for any Steiner triple system (with at least one edge). Thus, the study of  -colorings may be viewed as an attempt to understand snarks.
-colorings may be viewed as an attempt to understand snarks.
It is not hard to see, that a graph is Fano-colorable iff it has a nowhere-zero 8-flow. Thus (by Jaeger's result) Fano plane is "almost universal": it is possible to use it to color any bridgeless cubic graph (but it doesn't work for any graph with a bridge).
Grannell et al. [GGKS] constructed a universal Steiner triple system of order 381. Holroyd, Skoviera [HS] proved that neither projective nor affine Steiner triple systems are universal. Kral et al. [KMPS] proved that any non-affine non-projective non-trivial point-transitive Steiner triple system is universal.
Bibliography
*[GGKS] M.J. Grannell, T.S. Griggs, M. Knor, M. Skoviera, A Steiner triple system which colours all cubic graphs, J. Graph Theory 46 (2004), 15--24. MathSciNet
[HS] F. Holroyd and M. Skoviera, Colouring of cubic graphs by Steiner triple systems, J.~Combin. Theory Ser. B 91 (2004), 57--66.
[KMPS] D. Kral, E. Macajova, A. Por, J.-S. Sereni, Characterization results for Steiner triple systems and their application to edge-colorings of cubic graphs, preprint.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University