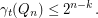The conjecture is false and it can be seen that this is so by using a computer program. For example which is not a power of two.
Alternatively we can argue as follows. For any graph we clearly have Now the bound by Alon and Spencer states In particular this implies that for any constant and large enough we have
The conjecture is false
The conjecture is false and it can be seen that this is so by using a computer program. For example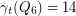 which is not a power of two.
which is not a power of two.
Alternatively we can argue as follows. For any graph we clearly have
we clearly have 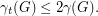 Now the bound by Alon and Spencer states
Now the bound by Alon and Spencer states 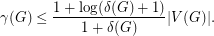 In particular this implies that for any constant
In particular this implies that for any constant 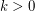 and large enough
and large enough  we have
we have