 login/create account
login/create account
 with minimum outdegree at least
with minimum outdegree at least  has a cycle with length at most
has a cycle with length at most 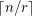
It is one of the most famous conjectures in graph theory. It has many alternative formulations and lots of work have been done around it. Many interesting conjectures are related to it. See [Sul]. It is in particular implied by a conjecture of Thomassé and Hoàng-Reed Conjecture.
The Caccetta-Häggkvist Conjecture is a generalization of an earlier conjecture of Behzad, Chartrand, and Wall, who conjectured it only for diregular digraphs. Caccetta-H äggkvist Conjecture has been proved for 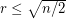 by Shen [She1]. For
by Shen [She1]. For 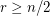 it is trivial. But already for
it is trivial. But already for 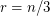 , it is still open as well as Behzad-Chartrand-Wall Conjecture
, it is still open as well as Behzad-Chartrand-Wall Conjecture
 -vertex digraph with minimum outdegree at least
-vertex digraph with minimum outdegree at least 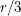 and minimum indegree at least
and minimum indegree at least 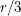 has a cycle with length at most
has a cycle with length at most  .
. This conjecture would be implied by Seymour's Second Neighbourhood Conjecure.
Shen [She2] also proved the following approximate version.
 with minimum outdegree at least
with minimum outdegree at least  has a cycle with length at most
has a cycle with length at most 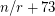 .
. Bollobás and Scott [BS] proposed a weighted version of the Caccetta-Häggkvist Conjecture.
![$ w:E(D) \rightarrow [0,1] $](/files/tex/43734b72b4366d8eddfad72bdffb0e71324d4505.png) be a weight function on the arcs of a digraph
be a weight function on the arcs of a digraph  . If
. If 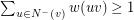 and
and 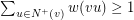 for all
for all  , then there is a directed cycle in
, then there is a directed cycle in  of total weight at least 1.
of total weight at least 1. They gave a nice proof that there is a directed path of total weight at least 1.
Bibliography
[BCW] M. Behzad, G. Chartrand, and C. Wall. On minimal regular digraphs with given girth. Fundamenta Mathematicae, 69:227–231, 1970.
[BS] B. Bollobás and A. D. Scott, A proof of a conjecture of {B}ondy concerning paths in weighted digraphs. J. Combin. Theory Ser. B, 66:283-292, 1996.
*[CH] L. Caccetta and R. Häggkvist. On minimal digraphs with given girth. Congressus Numerantium, XXI, 1978
[She1J. Shen. On the girth of digraphs. Discrete Math, 211(1-3):167–181, 2000.
[She2] J. Shen. On the Caccetta-Häggkvist conjecture. Graphs and Combinatorics, 18(3):645–654, 2002.
[Sul] Blair D. Sullivan: A Summary of Problems and Results related to the Caccetta-Häggkvist Conjecture
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University