 login/create account
login/create account
An antidirected tree is an orientation of a tree in which every vertex has either indegree 0 or outdergree 0.
 be a digraph. If
be a digraph. If 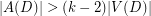 , then
, then  contains every antidirected tree of order
contains every antidirected tree of order  .
. The value 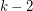 would be best possible, since the oriented tree consisting of a vertex dominating
would be best possible, since the oriented tree consisting of a vertex dominating 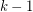 other vertices is not contained in any digraph in which every vertex has outdegree
other vertices is not contained in any digraph in which every vertex has outdegree 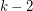 . The condition on the trees be antidirected cannot be suppressed. In a bipartite digraph
. The condition on the trees be antidirected cannot be suppressed. In a bipartite digraph  with bipartition
with bipartition 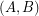 such that all arcs are directed from
such that all arcs are directed from  to
to 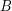 , all the trees contained in
, all the trees contained in  are antidirected.
are antidirected.
This conjecture for symmetric digraphs is equivalent to the celebrated Erdös-Sos conjecture for undirected graphs. (see [E]).
 be a graph. If
be a graph. If 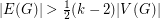 , then
, then  contains every tree of order
contains every tree of order  .
. Addario-Berry et al. Conjecture also implies Burr's conjecture (see Oriented trees in n-chromatic digraphs) for antidirected trees, since every digraph with chromatic number 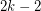 contains a colour-critical digraph has minimum degree at least
contains a colour-critical digraph has minimum degree at least 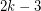 , and so whose number of vertices is at least
, and so whose number of vertices is at least 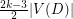 , which exceeds
, which exceeds 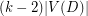 .
.
This conjecture has only been proved [AHL+] for antidirected trees of diameter at most  .
.
Bibliography
*[AHL+] L. Addario-Berry, F. Havet, C. Linhares Sales, B. Reed, and S. Thomassé. Oriented trees in digraphs. Discrete Mathematics, 313(8):967-974, 2013.
[E] P. Erdös, Some problems in graph theory, Theory of Graphs and Its Applications, M. Fielder, Editor, Academic Press, New York, 1965, pp. 29--36.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University